Introduction au formalisme de la mécanique quantique – WUS#32

J’ai mis longtemps avant de me décider à écrire un billet sur la physique quantique. Tout simplement parce que ça fait peu de temps que je fais de la mécanique quantique en cours (un peu moins de deux ans), et j’aime bien avoir du recul sur les sujets que je traite. Ce qui m’a frappé quand j’ai commencé à faire de la mécanique quantique c’est la différence entre mes cours et la manière dont le sujet est abordé en vulgarisation. C’est souvent le propre de la vulgarisation d’éluder la mathématisation pour évoquer les concepts physiques. Parce que – comme on l’a vu dans le billet précédent sur les équations de Maxwell – les équations peuvent être traduites et expliquées physiquement, en se basant notamment sur l’intuition. Sauf qu’en mécanique quantique, c’est différent, parce que c’est une théorie qui va profondément à l’encontre de notre intuition classique.

 

Si bien qu’il est difficile de faire émerger des concepts non mathématisés qui correspondent à la manière dont cette théorie quantique décrit les objets physiques. C’est pourquoi on va voir aujourd’hui les bases (mathématiques donc) du formalisme de la mécanique quantique, afin de vous montrer les outils qui permettent de construire la mécanique quantique, et ainsi de vous donner les moyens de voir autrement les concepts dont on entend souvent parler, à savoir la non-localité, le probabilisme, la dualité onde-corpuscule, la quantification. Attention, un billet un peu technique, mais que je me suis efforcé de rendre compréhensible ! Peu d’exemples, mais c’est fait exprès pour ne pas vous noyer dans le formalisme. Je veux juste vous donner les grandes idées de ce sur quoi repose vraiment la mécanique quantique. Ce billet s’adresse à un public un peu averti ou simplement curieux et motivé ! 🙂

Rappelons juste que la théorie quantique est une théorie – un modèle donc – qui permet de décrire le comportement de la matière aux très petites échelles. Cette théorie n’a pour l’heure jamais été mise en défaut. Ce n’est pas pour autant qu’il s’agit de la « vraie » théorie, permettant de décrire la nature mieux que les autres. Il s’agit d’un modèle incroyablement efficace, mais totalement inutile pour décrire par exemple la mécanique d’objets de notre taille. La mécanique newtonienne suffit dans ce cas, c’est pour ça qu’on se permet très souvent de modéliser une particule comme un point matériel. Parce que ça suffit. Il n’y a pas une meilleure manière absolue de décrire les choses. Tout dépend du domaine d’application.

Plutôt que d’introduire les concepts mathématiques et d’ensuite expliquer à quoi ça sert, je vais vous exposer les principes de base et leurs implications. Ça me semble plus vivant et plus pédagogique. Rappelons juste comme il est fait assez souvent qu’on ne discutera pas ici des implications philosophiques de ces différents principes (globalement c’est ce qu’on appelle l’approche de l’École de Copenhague – du nom de la ville où travaillait Niels Bohr à l’époque de l’établissement de ces principes). Dans toute la suite, on appellera « système quantique » un objet microscopique soumis aux lois de la mécanique quantique (typiquement un électron).

Comme à mon habitude dans les billets un peu théoriques, je vais agrémenter cet article de jolies images pour s’aérer le cerveau entre deux paragraphes 🙂 Ici, Copenhague.

Premier postulat : la description de l’état quantique d’un système

Un système quantique est complètement décrit à chaque instant par un vecteur d’état normé, noté , appartenant à un espace de Hilbert.

Qu’est-ce que ça veut dire ? Et bien ça veut dire qu’on peut connaître toutes les informations d’un système en connaissant son vecteur d’état. Imaginez comment vous vous représentez un vecteur dans un espace (euclidien) à trois dimensions. C’est une flèche, qui peut être de n’importe quelle longueur, dans n’importe quel sens, dans un espace 3D. Et bien un espace de Hilbert c’est essentiellement la même chose sauf que cette fois les composantes du vecteur peuvent être complexes (cf mon billet d’introduction aux nombres complexes) et de dimension quelconque. C’est donc plus difficile à se représenter évidemment. Comme un espace euclidien, un espace de Hilbert comporte un produit scalaire, qui permet de projeter un vecteur suivant un autre. Notons par ailleurs que l’on peut définir une norme du vecteur d’état (comme pour une flèche dans l’espace), et qu’on s’arrange pour que la norme d’un vecteur d’état soit toujours égale à 1 (pour une raison que l’on verra plus loin).

Si je résume : un système quantique se décrit dans un espace mathématique particulier, complexe. Il existe un vecteur de cet espace qui contient toute l’information sur le système.

Notons que l’on en déduit directement ce qu’on appelle le principe de superposition : si j’ai deux vecteurs appartenant à l’espace de Hilbert, alors leur somme appartient aussi à l’espace de Hilbert (comme la somme de deux vecteurs de l’espace donne toujours un vecteur de l’espace).

Toute la question va donc consister à savoir décrire judicieusement cet espace de Hilbert dans lequel évolue l’état quantique. Pour se repérer dans l’espace, on décompose l’espace euclidien en trois axes. C’est exactement ce qu’il s’agit de faire dans le cas hilbertien, à chaque fois on va essayer de déterminer une base pour décrire l’espace de Hilbert proprement et écrire le vecteur d’état judicieusement.

La notion de « ket » est juste une nouvelle notation pour décrire qu’un objet mathématique est un vecteur de l’espace des états. C’est pratique d’écrire un ket , puisque si on veut le projeter suivant le ket , il suffit de faire le produit scalaire (la projection) en écrivant , où est appelé un « bra ». La quantité est alors un nombre. C’est la projection de l’un sur l’autre. On appelle tout ça la notation « braket », développée par Paul Dirac.

Bristol, ville natale de Dirac.

Deuxième postulat : l’observable

Toute grandeur physique mesurable est associée à un opérateur linéaire hermitien appelé « observable ».

Qu’est-ce qu’une grandeur physique ? C’est une grandeur qui correspond à une quantité que l’on peut mesurer. La position, la vitesse, l’énergie par exemple. Et bien comment agissent ces grandeurs dans le formalisme de la mécanique quantique ? Comme le dit le principe, chaque grandeur que l’on peut mesurer est associée à un opérateur qui agit sur le vecteur d’état (un opérateur c’est comme une fonction). On note souvent une fonction réelle où est la variable réelle du problème. La fonction associe à chaque nombre un autre nombre . Ici il s’agit d’un raisonnement analogue : chaque observable transforme un vecteur d’état en un autre vecteur d’état de l’espace hilbertien (linéarité). Par exemple la mesure de l’énergie d’un système est associée à l’observable appelée le Hamiltonien du système. Cet opérateur comprend toutes les contraintes énergétiques agissant sur le système (force électrostatique de l’atome sur l’électron par exemple). L’opérateur agit sur le ket . Comme le ket en question est un vecteur, l’opérateur transforme chacune de ses composantes dans la base de l’espace hilbertien. Comme si une fonction réelle transformait un ensemble de points de l’espace à trois dimensions en un autre ensemble de points, sauf qu’ici on appelle la fonction observable (ou opérateur) et que l’espace est complexe. Cet opérateur possède des propriétés particulières, dites hermitiennes, qu’on ne détaillera pas ici.

Noter qu’un opérateur n’est pas un vecteur d’état. Ce n’est pas un objet mathématique qui a les mêmes dimensions. On peut souvent mettre une observable sous la forme d’une matrice (un tableau d’autant de colonnes que de lignes, remplie par des coefficients complexes), tandis qu’on représente souvent les vecteurs d’état en colonne, avec autant de lignes que de composantes de l’espace hilbertien.

Si je résume à ce stade, on a dit quelque chose qui ne paye pas de mine mais qui est assez fort : un système est entièrement décrit par un vecteur d’état, et à chaque grandeur physique on associe un opérateur qui agit sur le vecteur d’état.

Dublin, ville natale de William Rowan Hamilton.

Troisième postulat : le résultat d’une mesure

 Les résultats possibles de la mesure d’une grandeur physique sont les valeurs propres de l’observable associée.

Ah, alors là vous vous disez peut-être : mais quel est la différence avec ce qui précède ? En fait, ce qu’on vient de déterminer précédemment, c’est comment on associe une grandeur physique à la description d’un système. On applique au vecteur d’état un opérateur, ce qui nous donne un nouveau vecteur d’état. Mais désormais, ce principe nous donne ce qui se passe quand on fait expérimentalement la mesure de cette grandeur physique. Ce qui est dit ici, c’est qu’alors plusieurs résultats sont possibles ! C’est là qu’intervient le probabilisme de la mécanique quantique.

Dans un premier temps, on écrit mathématiquement l’observable. Si je reprends l’exemple du Hamiltonien (l’éngerie du système), cela revient à sommer tous les termes énergétiques modélisant les interactions avec l’extérieur notamment. On vient de dire qu’une observable peut alors s’écrire sous la forme d’une matrice, un tableau à N lignes et N colonnes. En fait, en mathématiques, il existe des bases privilégiées permettant d’écrire les matrices hermitiennes sous la forme de matrices diagonales, c’est-à-dire que tous les coefficients de la matrice sont nuls, sauf sur la diagonale. On parle de diagonalisation. Les valeurs diagonales de la matrice sont alors appelées valeurs propres de l’opérateur hermitien (ou bien de la matrice hermitienne, de manière équivalente). Ces valeurs propres correspondent aux résultats possibles de la mesure physique (ce sont toujours des valeurs réelles et non pas complexes, du fait des propriétés hermitiennes de l’observable). Et – précision cruciale – dans la mesure où il y a un nombre fini (ou plutôt dénombrable) de valeurs propres (ce qui arrive lorsque la matrice décrivant la grandeur physique n’est pas une matrice infinie), cela signifie que les résultats de la mesure sont quantifiés. S’il y a un nombre fini de valeurs propres alors il y a un nombre fini de résultats de mesures possibles ! C’est notamment le cas pour l’énergie très souvent (lorsque le système est soumis à des conditions aux limites par exemple), si bien qu’on voit alors émerger le concept de quantification de l’énergie.

L’énergie fonctionne donc par paliers !

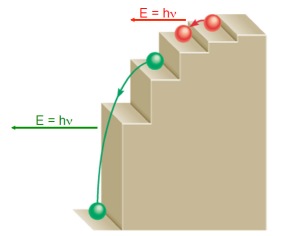
Ainsi, pour chaque grandeur physique correspondent des valeurs propres qui sont les résultats possibles de la mesure. Chaque valeur propre a une probabilité particulière d’être mesurée. C’est très puissant, parce que cela signifie que si on connaît la manière dont s’écrit l’observable (sous forme matricielle – ce qui arrive souvent), on peut grâce à une simple opération mathématique déterminer les résultats possibles de la mesure de la grandeur physique associée.

Quatrième postulat : la projection de mesure

Après une mesure, le système se trouve projeté dans l’état propre correspondant au résultat de la mesure.

Qu’est-ce que ça veut dire ? En fait, lorsqu’on diagonalise une matrice (une observable par exemple), à chaque valeur propre est associé ce qu’on appelle un état propre, qui correspond ici au vecteur d’état dans lequel a été « projeté » le vecteur d’état initial lors de la mesure. On peut dire qu’en quelque sorte dans la base de ces états propres (qui forment bien une base de l’espace hilbertien) on n’a gardé que la composante du vecteur d’état suivant l’état propre associé à la valeur propre mesurée. En clair, à chaque résultat possible de la mesure, le vecteur d’état après la mesure est un état bien déterminé.

Mettons qu’on mesure les résultats d’une observable . On mesure la valeur . Si on refait la même mesure de O, on retrouvera alors toujours le même résultat, avec une probabilité de 100%. En revanche, si on effectue une mesure de O, puis une mesure de B (une autre grandeur physique donc une autre observable), puis une mesure de O, alors le résultat peut varier. On peut écrire mathématiquement exactement l’état du système après la mesure, si on connaît le résultat. Ce n’est plus le même état qu’avant la mesure. On dit que la mesure perturbe le système quantique.

Pour déterminer la probabilité avec laquelle un résultat donné va être mesuré, il faut connaître le vecteur d’état initial, le vecteur d’état projeté associé à la mesure, en faire le produit scalaire (on projette l’état initial sur l’état mesuré) et en prendre le module, c’est-à-dire grosso modo le mettre au carré : , où est l’état initial et le vecteur propre associé à la valeur propre . On connaît ainsi la probabilité de mesurer chaque résultat possible. On peut alors calculer des probabilités de mesure à partir du vecteur d’état, et faire des vérifications expérimentales des résultats prédits par la théorie. Et ça marche redoutablement bien !

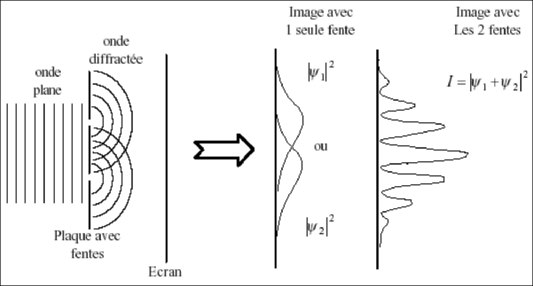
Notons à cette étape un résultat incroyablement important : ce n’est pas la probabilité de mesure qui est sommable, c’est le vecteur d’état. Prenez un exemple très connu, celui des fentes d’Young. Vous éclairez avec une lumière de couleur donnée une fente et regardez un écran derrière la fente. Vous observez une tache centrée derrière la fente. Maintenant prenez la même mesure, cachez la première fente et regarder le résultat à travers une autre fente un peu plus loin. Vous observez une tache, centrée derrière cette deuxième fente. Mais ensuite, faites la même chose avec les deux fentes ouvertes. Vous n’observez pas la somme des deux taches, mais une figure d’interférences pleine de strilles. Pourquoi ? Parce que ce n’est pas la probabilité de détecter de la lumière à un endroit qui se somme dans cette expérience, c’est le vecteur d’état associé à l’éclairement. C’est le vecteur d’état qui est linéaire. Pour calculer cette probabilité d’éclairement, on somme les deux vecteurs d’états et on élève au carré. Apparaît alors non seulement la somme des carrés (et donc les deux probabilités des expériences précédentes) mais aussi un terme supplémentaire dit d’interférences, qui explique la figure observée ! On n’additionne pas les probabilités en mécanique quantique.

L’expérience des fentes d’Young, via rpn.univ-lorraine.fr

Il était une fois le chat de Schrödinger : Imaginez qu’on mette un chat dans une boîte, et que la vie du chat dépende d’un détecteur de désintégration de particules. Ajoutons qu’une particule a une chance sur deux de se désintégrer au bout d’une minute. Cette particule peut se décrire par un vecteur d’état donné par la somme d’un état désintégré et d’un état non désintégré (les deux vecteurs propres !). Si la particule se désintègre, le chat meurt, sinon il reste en vie. Le chat est soit mort, soit vivant, ce sont les deux valeurs propres de l’observable associée. Quand on ouvre la boîte, alors avec une chance ½ le chat est vivant. Mais avant la première ouverture de la boîte, on ne saurait dire s’il était mort ou vivant. Dans le formalisme quantique, comme la particule, il est hypothétiquement l’un les deux. La vie du chat est conditionnée par le résultat de la mesure. Cet exemple a été mis en valeur pour montrer le paradoxe du formalisme quantique appliqué à des objets macroscopiques. On dit souvent que le chat est à la fois mort et vivant. Vous savez maintenant que c’est en fait le vecteur d’état du chat qui est la somme d’un vecteur d’état vivant et d’un vecteur d’état mort. Puis la mesure vient projeter l’état initial suivant l’un ou l’autre des résultats !

Cinquième postulat : l’évolution temporelle d’un système quantique

L’évolution temporelle du système quantique est donnée par l’équation de Schrödinger :

On a jusqu’ici décrit l’effet d’observables physiques sur un vecteur d’état, mais on s’intéresse maintenant à son évolution dans le temps. Il s’agit en fait ici d’une équation analogue au principe fondamental de la dynamique (la troisième loi de Newton), mais en beaucoup plus générale. est le vecteur d’état, qui comprend toutes les informations sur le système. est une observable qui comprend l’énergie du système. On l’appelle le Hamiltonien. Cette observable prend comme entrée le vecteur d’état. Ainsi on retrouve une relation entre la dérivée temporelle du vecteur d’état, et le vecteur d’état lui-même : il s’agit d’une équation différentielle, qui permet de déterminer l’évolution du vecteur d’état au court du temps. Ce résultat dépend des différentes énergies présentes dans le système.

Notons que est une constante appelée la constante de Planck réduite, et que est le nombre complexe dont le carré vaut . Il est tout à faire remarquable que cette équation, censée décrire le comportement de systèmes physiques, soit complexe. Mais comme on l’a vu, le vecteur d’état est complexe, et ce n’est qu’en repassant aux probabilités qu’on retrouve des résultats physiques, et donc réels (au sens de non complexes).

Bon alors ça paraît ensuite plutôt facile, il suffit de résoudre cette équation et on peut connaître le comportement de tout système quantique ! Oui sauf que non, car très souvent le Hamiltonien est très difficile à écrire ce qui rend l’équation parfois impossible à résoudre analytiquement (notamment quand il y a beaucoup de particules). Il faut alors faire des simulations numériques et/ou des approximations. Il y a des gens dont le métier consiste à écrire des Hamiltoniens !

On a vu à ce stade les principes fondamentaux de la mécanique quantique ! Description mathématique du système dans un espace hilbertien, description des grandeurs physique via des observables qui agissent sur le vecteur d’état, résultat de mesure probabiliste, quantification, projection de mesure, et équation de Schrödinger !

Vienne, ville natale d’Erwin Schrödinger.

Et le principe de Heisenberg ?

Vous savez, ce principe qui dit qu’on ne peut pas connaître avec une précision infinie à la fois la position et la vitesse d’un objet quantique ? Et bien je n’en parle pas, car le principe d’indétermination de Heisenberg n’est pas un principe dans ce formalisme. Il s’agit d’un résultat mathématique qui peut se démontrer, en écrivant les opérateurs position et impulsion (qui correspondent aux observables associés à la position et la vitesse des particules). On dit que ces opérateurs ne commutent pas, ils ne sont pas interchangeables dans un produit, ce qui se traduit physiquement par le fait qu’on ne peut pas les mesurer simultanément. Dans une formulation plus moderne on parle plutôt des relations de Heisenberg, mais bien que facile à montrer dans le cadre du formalisme présenté ci-dessus, ce résultat est tellement étonnant pour une intuition classique comme la nôtre que c’est un résultat totalement remarquable.

Wurtzbourg, ville natale de Werner Heisenberg.

Conclusion

Voilà, on a vu les bases de la mécanique quantique. Comme vous le voyez, c’est très mathématisé et assez éloigné de bon nombre de représentations qu’on en a. On s’imagine une théorie pleine d’aléatoire où on joue avec les concepts d’onde et de particule. Enfin c’était mon cas. Mais en fait, tout y est parfaitement établi à travers la notion de vecteur d’état agissant dans un espace complexe. Je ferai une autre fois un billet détaillant la notion d’intrication quantique dans ce contexte,  qui apparaît presque naturellement une fois qu’on déroule les principes ci-dessus et qu’on les applique dans des cas simples. Mais j’espère vous avoir donné un bon aperçu de ce qu’on fait en mécanique quantique, d’où on part et de ce qu’on cherche à faire. J’ai conscience que ce billet est un peu long et indigeste mais cela aurait eu relativement peu de sens de le faire en deux parties. J’espère qu’il pourra être utile aux curieux ayant quelques prérequis mathématiques et se demandant ce qu’est la mécanique quantique.

Pour des références un peu moins techniques on trouve un tas de bonnes explications sur Internet, je vous recommande par exemple ce très bon article de David Louapre de Science étonnante, encore une fois le très bon site http://tout-est-quantique.fr, et n’importe quel cours ou ouvrage de Claude Aslangul pour les plus audacieux.

 

Merci à Jean-François Roch.